
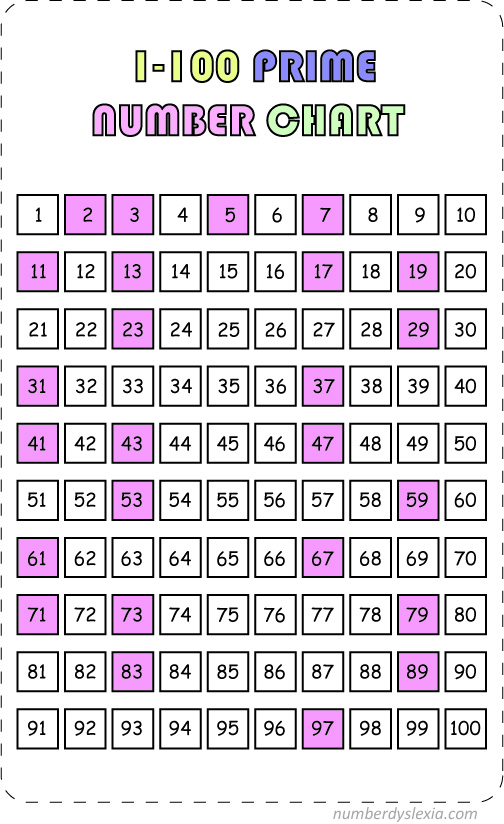
It follows that \( p_1 \) cannot divide \( m \) and similarly none of the \( p_j \) can divide \( m, \) all of whose prime divisors must therefore be other than \( p_1, p_2, \cdots p_n. \) That is, \( p_1 | 1 \) and therefore \( p_1 = 1, \) which is not a prime number. Then every prime divisor of \( m = p_1 \cdot p_2 \cdot p_3 \cdots p_n + 1 \) is different from \( p_1, p_2, \ldots p_n, \) so there is at least one more prime.
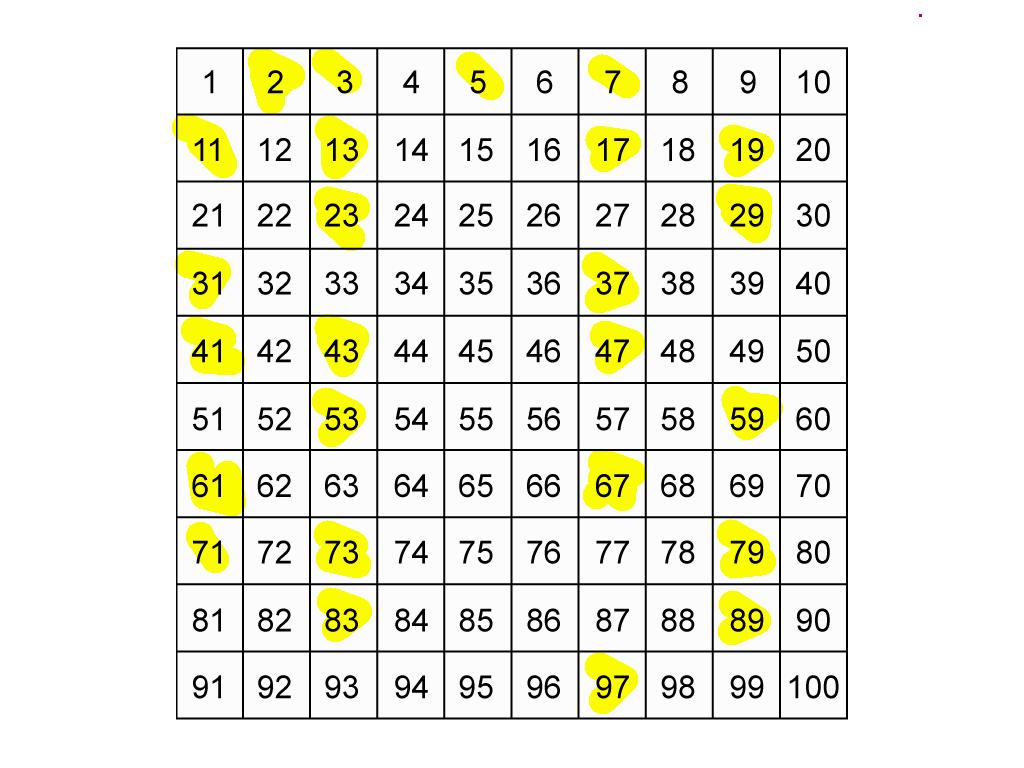
Suppose \( p_1, p_2, \ldots p_n \) represent the first \( n \) prime numbers: \( p_1 = 2, p_2 = 3, p_3 = 5, \) and so on. The modern proof goes like this: Theorem. Like all of Euclid, the proof is geometrical, with line segments representing numbers, but it's valid and recognizable. Euclid proved that there are infinitely many prime numbers in 300 BC in Book IX, Proposition 20 of the Elements. The key fact about the primes is that every natural number can be written as a product of primes, and the product is unique up to the order of the factors. These are the counting numbers having no divisors other than one and themselves: The prime numbers have been an object of fascination for a long time.


 0 kommentar(er)
0 kommentar(er)
